Regresi
linier seperti yang kita ketahui tidak dapat menyelesaikan kasus dimana
variabel dependent bersifat dikotomi dan kategori dengan dua atau lebih
kemungkinan (ex. sukses atau Gagal; terpilih atau tidak terpilih; lulus
atau tidak lulus; melakukan pembelian atau tidak; mendapat promosi atau
tidak, dan lain-lain). Regresi logistik umumnya melibatkan berbagai
macam variabel prediktor baik numerik ataupun kategorik, termasuk
variabel dummy. Pada regresi linier, variabel prediktor yang digunakan
biasanya numerik, tetapi jika kita melibatkan campuran antara numerik
maupun kategorik kita dapat menggunakan regresi logistik.
Regresi
logistik membentuk persamaan atau fungsi dengan pendekatan maximum
likelihood, yang memaksimalkan peluang pengklasifikasian objek yang
diamati menjadi kategori yang sesuai kemudian mengubahnya menjadi
koefisien regresi yang sederhana. Dua nilai yang biasa digunakan sebagai
variabel dependen yang diprediksi adalah 0 dan 1 (ex. 1=berhasil,
0=gagal).
Regresi logistik menghasilkan rasio peluang (odds ratios) antara
keberhasilan atau kegagalan suatu dari analisis. Dapat kita contohkan
dengan seorang tokoh yang ingin menjadi presiden, akan lebih baik
peluangnya jika menjadi ketua partai politik tertentu. Disini odds ratio
yang dimaksud adalah seberapa besar peluang tokoh tersebut dengan
mempertimbangkan variabel prediktor yang ada.
Regresi logistik akan membentuk variabel prediktor/respon (log (p/(1-p))
yang merupakan kombinasi linier dari variabel independen. Nilai
variabel prediktor ini kemudian ditransformasikan menjadi probabilitas
dengan fungsi logit.
Asumsi-asumsi dalam regresi logistik
- Tidak mengasumsikan hubungan linier antar variabel dependen dan independent
- Variabel dependen harus bersifat dikotomi (2 variabel)
- Variabel independent tidak harus memiliki keragaman yang sama antar kelompok variabel
- Kategori dalam variabel independent harus terpisah satu sama lain atau bersifat eksklusif
- Sampel yang diperlukan dalam jumlah relatif besar, minimum dibutuhkan hingga 50 sampel data untuk sebuah variabel prediktor (bebas).
Persamaan Regresi Logistik
Regresi logistik menghasilkan rasio peluang yang dinyatakan dengan
transformasi fungsi logaritma (log), dengan demikian fungsi transformasi
log ataupun ln diperlukan untuk p-value, dengan demikian dapat
dinyatakan bahwa logit(p) merupakan log dari peluang (odds ratio) atau
likelihood ratio dengan kemungkinan terbesar nilai peluang adalah 1,
dengan demikian persamaan regresi logistik menjadi:
logit(p) = log (p/1-p) = ln (p/1-p)
dimana p bernilai antara 0-1.
Model yang digunakan pada regresi logistik adalah:
Log (P / 1 – p) = β0 + β1X1 + β2X2 + …. + βkXk
Dimana p adalah kemungkinan bahwa Y = 1, dan X1, X2, X3 adalah variabel independen, dan b adalah koefisien regresi.
Konsep Log Odds, Odds Ratio
Logit (log odds) merupakan koefisien slope (b) dari persamaan regresi.
Slope disini adalah perubahan nilai rata-rata dari Y dari satu unit
perubahan nilai X. Regresi logistik melihat perubahan pada nilai
variabel dependen yang ditransformasi menjadi peluang, bukan nilai
aslinya seperti pada regresi linier. Sebagai ilustrasi jika nilai
peluang adalah 0,25, maka nilai odds adalah 3 (25 : 75), sedangkan jika
nilai peluang 50, maka nilai odds adalah 1 (50 : 50), atau jika nilai
peluang 0,33, maka nilai odds adalah 2 (33 : 67) dengan total
keseluruhan nilai peluang adalah 1. Nilai odds ratio biasanya dapat kita
lihat pada kolom B pada ‘variables in the equation’ output SPSS.
Kecocokan Model (model fit) dan fungsi likelihood
Likelihood berarti juga peluang atau probabilitas untuk hipotesis
tertentu. Seperti yang kita ketahui pada kurva regresi linier kita lihat
adanya hubungan linier, peningkatan pada sumbu Y akan diikuti dengan
peningkatan pada sumbu X dan sebaliknya. Tetapi pada regresi logistik
dengan nilai Y antara 0 dan 1, pendekatan linier tidak bisa kita
gunakan. Oleh karena itu metode maximum likelihood sangat berguna dalam
menentukan kecocokan model yang tepat bagi persamaan yang kita miliki.
Hipotesis dalam regresi logistik antara lain:
h0 = ketika persamaan regresi bernilai 0 [logit(p) = 0].
h1 = persamaan regresi berbeda nyata dari 0 [logit(p) ≠ 0].
Regresi logistik merupakan regresi non linier dimana model yang
ditentukan akan mengikuti pola kurva linier seperti gambar di bawah ini.
Regresi logistik juga menghasilkan rasio peluang (odds ratios) terkait
dengan nilai setiap prediktor. Peluang (odds) dari suatu kejadian
diartikan sebagai probabilitas hasil yang muncul yang dibagi dengan
probabilitas suatu kejadian tidak terjadi. Secara umum, rasio peluang
(odds ratios) merupakan sekumpulan peluang yang dibagi oleh peluang
lainnya. Rasio peluang bagi prediktor diartikan sebagai jumlah relatif
dimana peluang hasil meningkat (rasio peluang > 1) atau turun (rasio
peluang < 1) ketika nilai variabel prediktor meningkat sebesar 1
unit.
Lebih jelasnya kita dapat mengikuti ilustrasi berikut ini:
Kita ingin mengetahui apakah berat badan (weightgain) sapi para peternak
di kota elgrow bertambah signifikan atau tidak, dengan variabel
prediktor adalah sex yang terdiri atas male (M) atau female (F),
pemberian obat cacing (anthelmintic) secara rutin sesuai dosis yang
dinyatakan dengan yes dan no, dan biaya pemeliharaan per bulan yang
dinyatakan dalam US$. Kali ini kita akan menjalankan model logit
menggunakan bantuan software IBM SPSS versi 23, untuk yang masih
menggunakan SPSS seri di bawahnya jangan khawatir, masih kurang lebih
sama koq cara aplikasinya,
kamu bisa download datanya disini
kamu bisa download datanya disini
1. tahap impor data (misalnya dari excel), Buka SPSS kamu,
file > read text data,
pada kotak dialog open data, files of type > pilih excel, maka datanya muncul di layar, pilih lalu klik > open,
kemudian dimunculkan lagi jendela opening data, checklist seperti gambar > ok,
data telah masuk dalam record spss, berikut adalah dataview, lihat
sususannya tidak beraturan, kamu bisa atur dalam variable view:
atur label, desimal, dan lain-lain dalam variabel view,
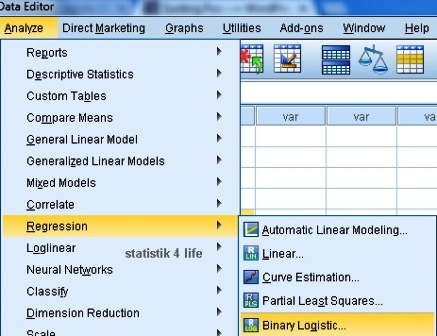
2. Tahap Analisis,
Analyze > regression > binary logistic,
Setelah muncul jendela logistic regression, masukkan weightgain kedalam
dependen, dan variabel kategorik yaitu sex dan anthelmintic ke kotak
covariates, lalu klik categorical, untuk menyesuaikan tipe data variabel
kategorik,
Di jendela define covariates variables pilih reference category first, kemudian klik changes > continue,
klik next lalu masukkan variabel kontinyu cost, ke dalam covariates, kemudian option,
kemudian continue > ok, maka outputnya akan ditampilkan,
- Chi-Square model sebesar 18,440, angka ini menjelaskan kemampuan model dalam memprediksi variabel dependen weightgain. Dengan signifikansi 0,000 < 0,05, berarti terdapat peningkatan signifikansi dengan penambahan variabel sex, dan anthelmintic, ke dalam model.
- -2 log likelihood menjelaskan signifikansi model layaknya R-sq pada regresi linier OLS.
- Tabel Hosmer and Lemeshow test menunjukkan nilai penambahan signifikansi model dari konstanta, dan model sesudah ditambahkan variabel independen sex dan anthelmintic. Penambahannya cukup kecil dengan signifikansi 0,631 (>0.05).
Kita lihat kembali pada output variables in the equation menunjukkan model sesuai hipotesis null atau model tanpa prediktor,
Output variables not in the equation menunjukkan signifikansi
masing-masing variabel independen terhadap weightgain. Dari tabel dapat
kita lihat bahwa variabel anthelmintic(1) memberikan peningkatan yang
signifikan terhadap model (0,000), sedangkan sex(1) tidak signifikan
(0,298). Tetapi secara keseluruhan signifikan terhadap perbaikan model
(overall statistics, sig = 0,000).
Dari output variables in the equation persamaan yang kita peroleh adalah (lihat nilai pada kolom B) :
Log odds(weightgain) = B0 + B1*sex(1) + B2*anthelmintic(1) + B3*cost
atau dengan nilai aslinya;
Log odds(weightgain) = -3,502 + 0,116*sex(1) + 2,638*anthelmintic(1) + 0,011*cost
Jika sex(1)=1 (lihat output coding), anthelmintic(1)=1 (lihat output coding), dan cost=US$ 100, maka persamaannya menjadi:
Log odds(weightgain) = -3,502 + 0,116(1) + 2,638(1) + 0,011(100)
Log odds(weightgain) = -3,502 + 0,116 + 2,638 + 1,1
Jika kita hilangkan log maka persamaan akan dalam bentuk eksponensial:
odds(weightgain) = e-3,502 + 0,116 + 2,638 + 1,1
Interpretasi dari Persamaan
- Untuk setiap perubahan per unit pada variabel sex(1) (koding dummy untuk variabel M/jantan), akan meningkatkan weightgain sebesar 0,116.
- Untuk setiap kenaikan pada variabel anthelmintic(1)sebesar 1 unit, maka akan meningkatkan weightgain sebesar 2,638.
- Untuk setiap penambahan sebesar US$1 terhadap variabel cost, maka akan meningkatkan peluang weightgain sebesar 0,011. Dari nilai signifikansi dapat kita simpulkan bahwa variabel yang signifikan berpengaruh terhadap log odds (weightgain) adalah pemberian obat cacing secara rutin (anthelmintic(1)), dan cost dengan nilai signifikansi berturut-turut 0,02 dan 0,018 (pada tingkat signifikansi 95%).
Kemudian mari kita interpretasikan nilai exp(B) pada output variables in the equation di atas:
- Variabel sex(1) yang mengacu pada Male/Jantan, memiliki kecenderungan untuk mendapatkan pertambahan berat badan (weightg ain) 1,122 kali daripada Female/betina yang menjadi kategori referensi kita (ini adalah koding dummy, dimana 0 untuk F dan 1 untuk M).
- Variabel anthelmintic(1) yang mengacu pada yes, dimana pemberian obat cacing secara teratur dan sesuai dosis memiliki peluang sebesar 13,988 kali daripada kategori referensi kita yang mengacu pada no, dimana no dinyatakan sebagai tidak memberikan asupan obat cacing secara rutin dan sesuai dosis. variabel ini sangat signifikan mempengaruhi log odds (weightgain) dengan nilai signifikansi 0,002.
- Variabel cost cenderung meningkatkan weightgain sebesar 0,030 kali dengan nilai signifikansi yang baik yaitu 0,018 < 0,05.(yoso)
























Social Plugin