Cara Baca Output Regresi Linear Berganda Data Sekunder

Bacaan Selanjutnya ...

Cara membaca Output Regresi berganda untuk data yang diolah dari sata sekunder sama dengan cara melihat output data primer, hanya saja dalam otput data sekunder kita mendapat tambahan uji Autokorelasi. Sedangkan selebihnya sama saja, posting ini saya buat untuk melengkapi posting saya tempo hari yang tidak sempat saya lanjutkan.

Baca: Cara Mengolah Data Sekunder (Data Angka) dengan SPSS dengan Regresi Linear Berganda

Adapun Output SPSS yang dihasilkan dari proses regresi linear berganda yang telah dilakukan tempo hari adalah:

Output Descriptive Statistics

Output pertama akan teman-teman lihat adalah Descriptive Statistic, disini kita disajikan data Mean (rata-rata), standar deviasi dan jumlah sampel yang diolah dari setiap variabel yang digunakan. Nilai standar deviasi yang dihasilkan secara umum harus lebih kecil dari nilai Mean, jika nilai Mean lebih kecil dari nilai standar deviasi memberikan informasi bahwa terdapat data atau bagian data yang tidak normal. Kemudian dibawahnya teman-teman akan melihat tabel Correlation:

Output Correlations

Pada tabel Correlations kita dapat melihat korelasi antar variabel dalam penelitian, data yang diperlihatkan adalah:

Pearson Correlations yang merupakan nilai R (Korelasi) yang menjadi tolak ukur hubungan antar variabel, semakin besar nilai Pearson Correlation maka semakin besar hubungan yang terjadi. Dari output diatas sekilas dapat dilihat bahwa tidak ada hubungan yang terlalu besar antara variabel independen yang ada dalam penelitian, korelasi yang tinggi dapat mencerminkan adanya multikolinieritas dalam penelitian
Sig. (1-Tailed) memperlihatkan kuat tidaknya hubungan antar variabel tersebut, hubungan dianggap kuat apabila nilai sig. diatas 0,05. Dalam output diatas terlihat bahwa nilai sig. yang dihasilkan umumnya masih dibawah 0,05 untuk setiap variabel bebas, ini juga menjadi penguat argumen bahwa tidak hubungan antar variabel dalam model yang terbentuk.
Baris N merupakan jumlah sampel yang diolah, disini sampel yang digunakan sebanyak 36 sampel.

Selanjutnya kita akan melihat output Variables Entered/Removed, disini kita diperlihatkan variabel-variabel apasaja yang dimasukkan ke model regresi dan apa saja yang dikeluarkan (biasanya ini terjadi dalam konsep penelitian eksperimental).

Output Variables Entered/Reoved

Dari Output diatas kita dapat lihat bahwa variabel-variabel independen yang dimasukkan adalah Dana Perimbangan, Ukuran, Kemakmuran dan Hutang serta variabel Kinerja Keuangan sebagai variabel dependen. Sedangkan metode yang digunakan olah data adalah enter artinya variabelnya dimasukkan oleh user sendiri.

Selanjutnya kita akan melihat output Model Summary, disini kita akan melihat seberapa besar pengaruh variabel independen secara umum terhadap variabel dependen dan juga hasil uji Autokorelasi.

Output Model Summary

Dari output diatas kita disajikan semua informasi yang penting untuk diperhatikan dan dipahami, hal ini terkait dengan kesimpulan penelitian teman-teman:

Kolom Model terdapat angka 1, hal ini memperlihatkan bahwa hanya terdapat satu model regresi yang terbentuk.
Kolom R (korelasi) memperlihatkan besarnya hubungan secara umum antar variabel independen dengan independen dalam output kali ini angka yang dihasilkan adalah 0,433 dengan demikian hubungan antar variabel indepeden dan dependen secara umum adalah 43,3% (0,433 x 100%) pada tingkat pertama.
Kolom R Square juga memperlihat nilai korelasi antar variabel independen dan dependen, perbedaannya dengan kolom R adalah nilai ini cenderung lebih akurat dikarenakan nilai ini berada pada tingkat kedua. Dalam kolom tersebut teman-teman dapat melihat ada anagka 0,188 sehingga hubungan antar variabel independen dan dependen adalah 18,8% (0,188 x 100%).
Kolom Adjusted R Square memberikan kita nilai yang paling akurat karena nilai ini berada pada tingkat ketiga. Dalam Model Summary teman-teman bisa melihat terdapat angka 0,083 artinya pengaruhnya sebesar 8,3% (0,083 x 100%).
Selanjutnya dalam Model Summary juga terdapat Kolom Durbin-Watson, nilai ini tidak terkait dengan besarnya pengaruh variabel independen terhadap dependen namun terkait dengan uji Asumsi Klasik yaitu Uji Autokorelasi. Dalam otput kali ini kita bisa liat terdapat angka 0,357. Dasar pengambilan keputusan terjadi tidaknya Autokorelasi yang saya gunakan disini adalah

Jika nilai D-W = +2 maka terdapat masalah autokorelasi negatif.
Jika nilai D-W = -2 maka terdapat masalah autokorelasi positif

Karena nilai D-W dalam penelitian ini adalah 0,357 maka nilai tersebut berada diantara +2 dan -2 sehingga tidak terjadi masalah autokorelasi dalam penelitian ini. Pengambilan keputusan nilai D-W ini juga dapat dilakukan dengan membandingkan nilai D-W hitung ini dengan nilai D-W di tabel D-W.

Selanjutnya kita beralih ketabel Anova, disini kita diperlihatkan nilai regresi linear berganda secara besama-sama dalam bentuk nilai F, sehingga banyak yang mengatakan ini hasil uji F:

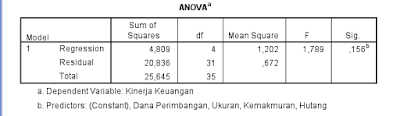Output Anova

Dari tabel Anova kita dapat melihat pada kolom Sum of Square memperlihat banyaknya nilai data yang dihitung, kemudian terdapat nilai df (degre of freedom) dan nilai signifikansi (probabilitasnya) adapun penjelasannya sebagai berikut:

Kolom Sum of Square memperlihatkan banyaknya nilai data yang diolah secara umum perbaris data, dalam output disini secara total terdapat angka 25,645, residual sebesar 20,835 dan Regression sebesar 4,809.
Kolom df (derajat kebebasan) dalam output kali ini sebesar 35, nilai ini diperoleh dari rumus df = n-1 =36 - 1 = 35.
Kolom Mean Square memperlihatkan jumlah nilai rata-rata nilai yang diolah tersebut.
Kolom F memperlihatkan nilai F yang dijadikan tolak ukur dalam uji F, semakin besar nilai F maka semakin besar bengaruh secara simultan. Dalam output kali ini nilai F sebesar 1,789 masih cukup kecil untuk dainggap berpengaruh. Tolak ukur berpengaruh tidaknya nilai uji juga dapat dilakukan dengan membandingkannya dengan nilai F tabel.
Kolom Sig. atau probabilitas memperlihatkan tingkat signifikansi, dimana nilai ini juga dijadikan nilai cut off untuk menilai berpengaruh tidaknya variabel-variabel indepeden terrhadap dependen. Jika nilai tersebut dibawah 0,05 (α) maka berpengaruh jika sebaliknya tidak berpengaruh.

Selesai dengan tabel Anova kita beralih ke tabel Coefficients, disini kita diberi informasi yang cukup detil tentang pengaruh pervariabel terhadap variabel dependen.

Output Coefficients

Dari tabel Coefficients kita bisa melihat banyak hal terkait gambaran pengaruh setiap variabel independen terhadap variabel dependen secara satu persatu. Tabel ini juga membeerikan informasi mengenai lolos tidaknya Uji Multikolinieritas dalam Uji Asumsi Klasik melalui nilai Tolerance dan VIF. Berikut perinciannya satu persatu:

Pada Kolom Unstandarized Coefficients kita dapat memperoleh dua jenis informasi, yaitu nilai coefficient itu sendiri dan standar errornya. Dari output diatas kita dapat lihat nilai coefficient dari masing masing sebagai berikut:

Koefisien Constant (Konstanta) sebesar 3,459 dengan standar error yang cukup tinggi yaitu 24,236.
Variabel Ukuran memiliki koefisien sebesar -0,365 dengan standar error 0,729.
Variabel kemakmuran memiliki koefisien 0,199 dengan standar error 0,312,
Variabel hutang memiliki koefisien -0,007 dengan standar error 0,174.
Variabel dana perimbangan memiliki koefisien sebesar 0,195 dengan standar error 0,310.

Dengan demikian Model Regresi yang terbentuk dari berbagai angka diatas adalah:

Y = 3,459 - 0,365X1 + 0,199X2 - 0,007X3 + 0,195X4 + e

Pada Kolom Standarized Coefficients kita disajikan informasi mengenai nilai Beta dari stiap variabel independen yang ada. Namun dalam analisis regresi linear berganda informasi tersebut tidak dipakai. Nilai beta tersebut digunakan dalam Path Analysis atau analisis jalur.

Baca: Mengolah Data Kuesioner Variabel Intervening dengan SPSS (Path Analysis)

Pada kolom t kita mendapat informasi mengenai besarnya nilai t per variabel independen, nilai t yang oleh sebagian orang dijadikan sebagai tolak ukur melihat pengaruh per variabel (parsial) dengan cara membandingkannya dengan nilai t tabel, dengan dasar pengambilan keputusan jika nilai t hitung lebih besar berati berpengaruh dan jika sebaliknya maka tidak berpengaruh.
Kolom Sig memberi kita informasi mengenai tingkat signifikansi setiap variabel independen untuk menentukan berpengaruh tidaknya variabel tersebut terhadap variabel dependennya. Dasar pengambilan keputusannya adalah apabila nilai signifikansi tersebut dibawah 0,05 (α) maka kesimpulannua berpengaruh jika diawah maka tidak berpengaruh.
Kolom Collinearity Statistic memberi kita informasi mengenai lolos tidaknya model regresi linear berganda disini dalam uji Multikilinearitas. Disini terdapat data tentan VIF (variance influenced factor) dan Tolerance.

VIF (variance influenced factor) adalah nilai varian yang dipengaruhi oleh factor lain selain disinya sendiri artinya dipengaruhi oleh variabel independen lainnya. Nilai ini harus lebih kecil dari 10, jika diatas 10 maka telah terjadi multikolinearitas. Dari hasil diatas terlihat bahwa seluruh variabel independen memiliki VIF dibawah 10.
Tolence adalah nilai pengaruh antar variabel indpenden yang dapat ditoleransi dalam statistik. Nilai ini harus berada diatas 0,1 semakin tinggi semakin bagus, jika berada dibawah 0,1 maka terjadi multikolinearitas. Dalam otput diatas seluruh variabel memiliki nilai tolerance diatas 0,1.

Selanjutnya kita beralih ke grafik, grafik yang pertama yang akan kita lihat adalah grafik histogram, grafik histogram ini memberi informasi mengenai uji Normalitas.

Grafik Histogram

Dari grafik diagram batang diatas kita dapat melihat bahwa batang-batang yang terbentuk cukup berantakan, hal ini menandakan adanya salah satu data variabel yang bermasalah. Namun dalam regresi linear berganda kita hanya melihat pada normalitas data seluruh variabel maka hal ini tidak perlu dipermasalahkan. Kriteria diangram batang yang dikatakan lolos uji normalitas adalah apabila batang-batang yang terbentuk mengikuti bentuk gelombang atau lonceng yang terdapat disitu. Pada output diatas meski cukup terlihat berantakan namun masih bisa dikatakan mengikuti garis gelombang tersebut.

Selanjutnya kita masuk ke grafik scatterplot, grafik scatterplot ini berisi titik yang membentuk pola tertentu berdasarkan data yang ada.

Grafik Scatterplot

Dari grafik scatterplot diatas juga dapat memberi kita informasi mengenai lolos tidaknya dalam uji Normalitas. Cara penilaiannya adalah apabila titik-titik tersebar mengikuti garis miring (diagonal) maka data disebut normal, jika melenceng jauh maka itu tandanya tidak normal.

Penilaian dengan metode grafik memang memiliki kelemahan dalam akurasinya, mengingat penilaiannya dilakukan melalui visual yang kadang kala terjadi perbedaan antara satu orang dengan yang lainnya. Untuk itu saya menyarankan teman-teman untuk mengukur normalitas ini dengan uji statistik seperti Kolmogorov-Smirnov dan kawan-kawannya.

Baca: Cara Melakukan Uji Normalitas dengan Statistik (Uji Kolmogorov-Smirnov)

Selanjutnya kita masuk ke scatterplot yang lebih aduhai yaitu scaterplot yang digunakan untuk uji Heteroskedastisitas.

Grafik Scatterplot Heroskedastisitas

Uji heteroskedastisitas ini dugunakan untuk melihat kesesuaian pengamatan dari waktu-kewaktu, model regresi seharusnya homokedastisitas, artinya pengamatan residualnya harus konsisten. Untuk melihat ada tidak heteroskedastisitas ini digunakan kriteria apa bila terdapat pola khusus seperti bergelombang naik dan turun maka terjadi heteroskedastisitas. Dari output diatas nampak terjadi heteroskedastisitas namun ini adalah penilaian visual yang dapat saja berbeda dengan oarang lain yang melihat, maka saya menyarankan untuk menggunakan pengujian heteroskedastisitas dengan statistik uji park, uji glejser atau uji white agar jelas karena terdapat nilai cut off yan baku.