Pada artikel kali ini, kita akan membahas mengenai Uji Hipotesis, yang mana uji tersebut banyak dipakai pada saat penelitian yang dilakukan dalam penyusunan Skripsi, Tesis maupun penelitian lainnya.
Hipotesis dapat didefinisikan sebagai pernyataan mengenai sesuatu yang perlu diuji kebenarannya. Untuk mengetahui kebenaran pernyataan tersebut, perlu dilakukan penelitian dan analisis. Pada kenyataannya, sebagian besar penelitian dilakukan menggunakan sampel. Dengan begitu, data hasil pengukuran sampel akan digunakan untuk menyimpulkan kebenaran suatu hipotesis.
| KESIMPULAN | HIPOTESIS | |
| BENAR | SALAH | |
| TOLAK | Kesalahan Type I | Tepat |
| TERIMA | Tepat | Kesalahan Type II |
Rangkaian proses sebagaimana disebutkan diatas, tidak serta merta dapat memberikan kepastian tentang hakikat benar atau tidaknya suatu hipotesis. Uji hipotesis berdasarkan pengamatan sampel hanya akan memutuskan apakah hipotesis akan diterima atau ditolak. Dengan prosedur seperti itu, seorang peneliti dalam proses pengambilan keputusan akan menghadapi dua kemungkinan kesalahan, yaitu Kesalahan Type I dan Kesalahan Type II.
Tabel diatas memberikan makna bahwa seorang peneliti berharap dapat membuat kesimpulan yang tepat dalam menerima atau menolak suatu hipotesis. Oleh karenanya, dalam melakukan pengujian hipotesis, peneliti tersebut harus memiliki aturan main atau metodologi yang tepat. Salah satu aturan main yang dapat digunakan adalah dengan membandingkan nilai statistik dengan harga parameter yang dihipotesiskan. Jika perbedaan kedua harga ini cukup kecil maka hipotesis diterima, sedangkan jika perbedaan cukup besar maka hipotesis ditolak.
Ha = Hipotesis Alternatif
Ho = Hipotesis Nol (nihil)
Selanjutnya kita akan membahas mengenai Uji rata-rata, apa yang dimaksud dengan Uji rata-rata tersebut?
Uji rata-rata dimaksudkan untuk menentukan apakah dugaan tentang parameter suatu populasi didukung kuat oleh informasi sampel atau tidak. Jika sebaran data mengikuti distribusi normal, ukuran sampel yang relatif kecil (n < 30) dan nilai standar deviasi populasi tidak diketahui, kita dapat memakai uji t dengan formulasi/rumus sebagai berikut :
Sedangkan jika distribusi data tidak diketahui, kita harus menggunakan sampel n > 30 sehingga data akan mendekati distribusi normal. Untuk n > 30 dapat menggunakan uji z dengan formula/rumus sebagai berikut :
Contoh kasus :
Sebuah Grossir menerima kiriman kaleng sereal dari sebuah supplier. Menurut informasi yang diterima dari pihak supplier, berat kaleng rata-rata adalah 16 gr. Pihak grossir tidak serta merta percaya lalu melakukan pengujian terhadap 10 sampel kaleng sereal secara acak sebelum menerima kiriman barang dalam mobil box pengangkutnya. Berikut data hasil pengamatan 10 sampel pada suatu hari kiriman barang.
| Nomor Sampel | Berat Sereal (gr) |
| 1 | 14,42 |
| 2 | 17,23 |
| 3 | 15,84 |
| 4 | 14,46 |
| 5 | 16,78 |
| 6 | 16,02 |
| 7 | 16,44 |
| 8 | 15,69 |
| 9 | 15,88 |
| 10 | 17,26 |
Lakukan analisis untuk menguji apakah hasil pengujian berat kaleng sereal yang dilakukan oleh pihak grossir sama dengan keterangan pihak supplier?
1. Formulasi hipotesisnya
Ho : X = µo
Ha : X = µo
Dimana µo = 16
2. Hitung rata-rata sampel
3. Hitung nilai standar deviasi sampel
4. Hitung nilai t
5. Tentukan nilai t tabel
Dengan menggunakan tabel t pada α/2 dan derajat bebas (degree of freedom) (df = n -1). Dengan menggunakan tabel t diperolah nilai t tabel adalah 2,262157
Tabel t
6. Penentuan kriteria uji
Langkah selanjutnya adalah kita harus membandingkan nilai t hitung dengan t tabel.
Jika t hitung > t tabel, maka Ho ditolak, artinya nilai rata-rata yang diharapkan berbeda dengan nilai rata-rata pengukuran sampel. Demikian sebaliknya, jika t hitung < t tabel maka Ho diterima atau dapat dikatakan rata-rata yang dibandingkan adalah sama.
7. Pengambilan keputusan
Berdasarkan tabel t diketahui t(0,05/2, 10-1) adalah 2,262157, karena nilai t hitung < t tabel maka Ho diterima dan Ha ditolak. Dengan demikian, dapat disimpulkan bahwa berat kaleng sebesar 16 gr sebagaimana dikatakan pihak supplier tidak berbeda nyata dengan hasil pengukuran menggunakan sampel oleh pihak grossir.
Perhitungan manual versi II
Metode ini dilakukan dengan mencari Confident Interval of Difference (CID), yaitu selisih dua rata-rata yang dibandingkan. Rumus nilai CID adalah sebagai berikut :
Langkah penyelesaian ;
1. Hitung nilai standard error
2. Tentukan tabel t
3. Hitung CID
(16,002 - 16) – 2,26216 * 0,3145890 ≤ D ≤ (16,002 – 16) + 2,26216 * 0,3145890
– 0,70965 ≤ D ≤ 0,71365
4. Kriteria Uji
Jika dalam CID terdapat Nol berarti Ho diterima dan Ha ditolak, sebaliknya jika dalam CID tidak terdapat nilai nol berarti Ho ditolak dan Ha diterima
5. Pengambilan keputusan
Karena nilai interval CID di dalamnya terdapat nilai nol, maka dapat disimpulkan bahwa Ho diterima, artinya pada tingkat keyakinan 95%, rata-rata pengukuran sampel oleh pihak grossir tidak berbeda nyata dengan dengan keterangan dari pihak supplier.
Penyelesaian dengan SPSS
1. Buat variabel Berat pada variable view
2. Pada data view, ketik nilai pengamatannya dengan nilai 14,42, 17,23 s/d 17,26 seperti pada gambar dibawah ini :
3. Pada menu Analyze pilih Compare Means > One Sample T Test seperti berikut :
4. Maka setelah proses tersebut dilakukan akan muncul tampilan sebagai berikut :
Pindahkan variabel ke sebelah kanan dan pada test value isi dengan nilai 16, kemudian klik tombol option isi Confident Level dengan 95
Klik tombol Continue dan klik OK, maka akan tampil report SPSS sebagai berikut :
| One-Sample Statistics | ||||
| | N | Mean | Std. Deviation | Std. Error Mean |
| Berat | 10 | 16.0020 | .99482 | .31459 |
| One-Sample Test | ||||||
| | Test Value = 16 | |||||
| | t | df | Sig. (2-tailed) | Mean Difference | 95% Confidence Interval of the Difference | |
| | Lower | Upper | ||||
| Berat | .006 | 9 | .995 | .00200 | -.7096 | .7136 |
5. Hasil perhitungan SPSS sama dengan perhitungan manual, dimana nilai mean menyatakan rata-rata sampel X = 16,002 dengan standard error Sx = 0,31459.
Nilai t hitung = 0,006 nilai p(t) = 0,995 dan CI Difference sebesar 0,7096 ≤ D ≤ 0,7136.
6. Pengambilan keputusan
Karena CID melewati titik nol maka rata-rata yang dibandingkan adalah tidak signifikan atau Ho diterima.
Selain menggunakan t hitung dengan tabel t dan CID, kita juga dapat menggunakan sig of (t two tail) yang sebenarnya merupakan luas daerah dibawah kurva yang dibatasi oleh –t dan t. Seperti pada gambar dibawah ini
7. Dari gambar diatas diketahui bahwa nilai sig of (t two tail) adalah nilai probabilitas dibawah kurva normal yang dibatasi oleh nilai t hitung p(t). Jika nilai sig > α maka Ho diterima dan Ha ditolak. Sebaliknya jika sig ≤ α maka Ho ditolak dan Ha diterima.
Karena nilai p(t) lebih besar dari α (0,05 ) maka nilai ini berada pada wilayah terima Ho. Dengan demikian, Ho diterima dan Ha ditolak. Atau dapat disimpulkan bahwa pada tingkat keyakinan 95% nilai pengamatan berat kaleng yang dilakukan oleh pihak grossir sama dengan keterangan dari pihak supplier.
Demikian pembahasan mengenai Uji Hipotesi Rata-rata yang dilakukan secara perhitungan manual dan SPSS, semoga bermanfaat bagi pengunjung blog ini.


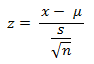





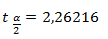

















Social Plugin